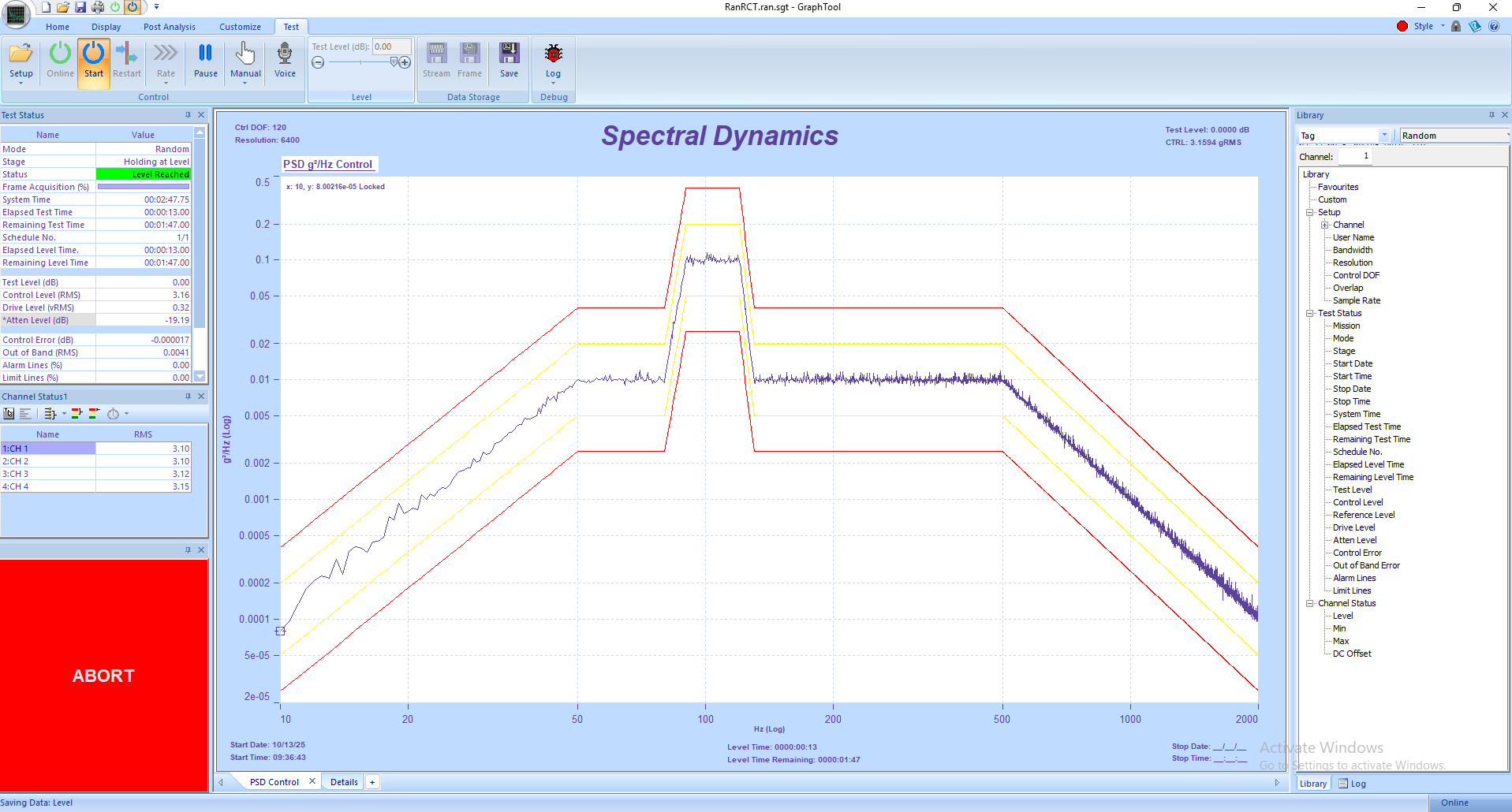
Statistical degrees of freedom (DOF) in random vibration analysis quantifies the confidence in a Power Spectral Density (PSD) estimate by relating it to the number of independent data frames used in the Fast Fourier Transform (FFT). A higher DOF means a more stable and accurate PSD estimate, which can be calculated using a chi-squared distribution to determine the probability that the test is within tolerance. For stationary Gaussian random vibration, DOF equals 2×F, where F is the number of time-data frames.
How it works
• Random Vibration and PSD: Random vibration involves random oscillations that can only be analyzed statistically. The PSD is a statistical tool that describes the frequency content of this random vibration, showing the power of the signal at each frequency.
• Averaging and FFT: To get a stable PSD estimate, multiple frames of time-history data are analyzed using the FFT and then averaged.
• Statistical Confidence: The average PSD is a chi-squared distributed random variable, and the degrees of freedom (DOF) determine how confident you can be in that estimate.
• The DOF Calculation: For a stationary, Gaussian random waveform, the DOF is calculated as 2×F, where 𝐹 is the number of independent time-data frames.
• More Frames = More DOF: A larger number of frames leads to a higher DOF and a smoother, more accurate PSD estimate.
• Overlap and Windowing: Techniques like frame overlap or window functions can introduce redundancy, which affects the DOF calculation. The DOF no longer equals 2×𝐹 in these cases.
• Probability and Tolerance: The DOF can be used to calculate the probability that the test is meeting its tolerance band, which is important for avoiding over- or under-testing.